Dalam dunia matematika, operasi matriks memainkan peran penting dalam memecahkan masalah kompleks di berbagai bidang. Contoh soal operasi matriks memberikan dasar yang kuat untuk memahami konsep ini dan menerapkannya secara efektif.
Contoh soal operasi matriks mencakup berbagai jenis operasi, seperti penjumlahan, pengurangan, perkalian, dan perkalian skalar. Dengan mempelajari langkah-langkah penyelesaian secara mendalam, siswa dapat menguasai teknik-teknik yang diperlukan untuk menyelesaikan masalah yang lebih kompleks.
Jenis-jenis Operasi Matriks

Operasi matriks merupakan manipulasi matematika yang dilakukan pada matriks, yang merupakan susunan bilangan yang diatur dalam baris dan kolom. Operasi-operasi matriks ini meliputi penjumlahan, pengurangan, perkalian, dan perkalian skalar.
Penjumlahan dan Pengurangan Matriks
Penjumlahan dan pengurangan matriks dapat dilakukan jika matriks-matriks yang dioperasikan memiliki jumlah baris dan kolom yang sama. Operasi ini dilakukan dengan menjumlahkan atau mengurangkan elemen-elemen yang terletak pada posisi yang sama pada kedua matriks.
Contoh:
| 1 | 2 |
| 3 | 4 |
+
Contoh soal operasi matriks menguji pemahaman dasar operasi aljabar matriks. Sementara itu, contoh soal jurnal penjualan memberikan latihan dalam pencatatan transaksi penjualan dalam akuntansi. Kembali ke contoh soal operasi matriks, penyelesaiannya melibatkan penerapan sifat-sifat operasi matriks seperti penjumlahan, pengurangan, dan perkalian.
Dengan menguasai operasi matriks, individu dapat menerapkannya dalam berbagai bidang, seperti fisika, teknik, dan ilmu komputer.
| 5 | 6 |
| 7 | 8 |
=
| 6 | 8 |
| 10 | 12 |
Perkalian Matriks
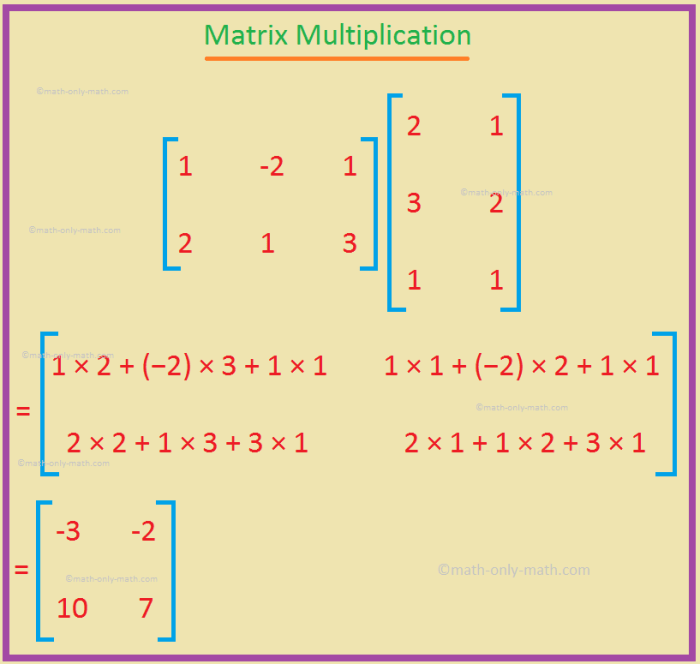
Perkalian matriks melibatkan penggandaan elemen-elemen baris dari matriks pertama dengan elemen-elemen kolom dari matriks kedua, kemudian menjumlahkan hasilnya. Hasil perkalian matriks adalah matriks baru dengan jumlah baris sama dengan matriks pertama dan jumlah kolom sama dengan matriks kedua.
Contoh:
| 1 | 2 |
| 3 | 4 |
×
| 5 | 6 |
| 7 | 8 |
=
| 19 | 22 |
| 43 | 50 |
Perkalian Skalar, Contoh soal operasi matriks
Perkalian skalar melibatkan penggandaan setiap elemen matriks dengan suatu bilangan, yang disebut skalar. Hasil perkalian skalar adalah matriks baru dengan jumlah baris dan kolom yang sama dengan matriks awal.
Contoh:
| 1 | 2 |
| 3 | 4 |
× 3=
| 3 | 6 |
| 9 | 12 |
Prosedur Operasi Matriks
Operasi matriks merupakan proses memanipulasi matriks sesuai dengan aturan tertentu. Dua operasi dasar pada matriks adalah penjumlahan dan pengurangan.
Dalam memahami operasi matriks, terdapat beragam contoh soal yang dapat membantu mengasah pemahaman. Selain itu, dalam menguasai bahasa Inggris, contoh soal contoh soal article a an the juga berperan penting untuk meningkatkan keterampilan berbahasa. Dengan mempelajari kedua jenis contoh soal ini, individu dapat memperkuat kemampuan berpikir logis dan linguistik mereka secara bersamaan.
Dengan demikian, penguasaan contoh soal operasi matriks tidak hanya bermanfaat untuk matematika, tetapi juga dapat berkontribusi pada pengembangan keterampilan bahasa Inggris.
Penjumlahan dan Pengurangan Matriks
Penjumlahan dan pengurangan matriks hanya dapat dilakukan jika matriks memiliki jumlah baris dan kolom yang sama. Berikut prosedur penjumlahan dan pengurangan matriks:
- Letakkan matriks yang akan dioperasikan berdampingan.
- Tambahkan atau kurangkan elemen matriks yang berada pada posisi yang sama.
- Hasil penjumlahan atau pengurangan akan membentuk matriks baru dengan jumlah baris dan kolom yang sama dengan matriks awal.
Sebagai contoh, misalkan kita memiliki dua matriks:
A = \beginbmatrix 1 & 2 \\\ 3 & 4 \endbmatrix, B = \beginbmatrix 5 & 6 \\\ 7 & 8 \endbmatrix
Maka penjumlahan dan pengurangan kedua matriks tersebut adalah:
A + B = \beginbmatrix 1 + 5 & 2 + 6 \\\ 3 + 7 & 4 + 8 \endbmatrix = \beginbmatrix 6 & 8 \\\ 10 & 12 \endbmatrixA
- B = \beginbmatrix 1
- 5 & 2
- 6 \\\ 3
- 7 & 4
- 8 \endbmatrix = \beginbmatrix
- 4 &
- 4 \\\
- 4 &
- 4 \endbmatrix
Aplikasi Operasi Matriks: Contoh Soal Operasi Matriks

Operasi matriks memiliki banyak aplikasi di berbagai bidang kehidupan nyata. Mereka digunakan untuk memecahkan masalah kompleks di bidang teknik, ekonomi, dan sains.
Contoh soal operasi matriks menguji pemahaman siswa tentang manipulasi matriks. Sebagai contoh, siswa mungkin diminta untuk menghitung determinan matriks atau menyelesaikan sistem persamaan linear menggunakan matriks. Di sisi lain, contoh soal contoh soal descriptive text essay mengharuskan siswa untuk menulis deskripsi yang jelas dan terstruktur tentang suatu topik.
Meskipun berbeda, kedua jenis soal ini menekankan pentingnya memahami konsep dasar dan menerapkannya dalam konteks yang berbeda. Contoh soal operasi matriks, misalnya, dapat membantu siswa mengasah keterampilan aljabar linier mereka, sementara contoh soal descriptive text essay dapat meningkatkan kemampuan menulis dan berpikir kritis mereka.
Aplikasi dalam Teknik
- Analisis struktur: Matriks digunakan untuk menganalisis beban dan tegangan pada struktur, seperti jembatan dan gedung.
- Rancangan sirkuit: Matriks digunakan untuk menganalisis dan merancang sirkuit listrik, seperti filter dan amplifier.
- Kontrol sistem: Matriks digunakan untuk mengontrol sistem dinamis, seperti robot dan pesawat.
Aplikasi dalam Ekonomi
- Analisis input-output: Matriks digunakan untuk menganalisis hubungan antar industri dalam perekonomian.
- Peramalan ekonomi: Matriks digunakan untuk meramalkan tren ekonomi, seperti tingkat inflasi dan pertumbuhan PDB.
- Optimasi portofolio: Matriks digunakan untuk mengoptimalkan portofolio investasi dengan mempertimbangkan risiko dan pengembalian.
Aplikasi dalam Sains
- Fisika: Matriks digunakan untuk mewakili transformasi linier, seperti rotasi dan translasi.
- Kimia: Matriks digunakan untuk merepresentasikan orbital atom dan molekul.
- Biologi: Matriks digunakan untuk menganalisis data genetik dan biologis lainnya.
Memecahkan Masalah Kompleks
Operasi matriks membantu memecahkan masalah kompleks dengan menyediakan kerangka kerja matematis yang dapat digunakan untuk:
- Merepresentasikan sistem dengan cara yang terstruktur dan ringkas.
- Menerapkan operasi aljabar dan kalkulus pada sistem tersebut.
- Menganalisis perilaku sistem dan memprediksi hasilnya.
Dengan demikian, operasi matriks menjadi alat yang sangat penting dalam berbagai bidang, memungkinkan kita untuk memahami dan memecahkan masalah kompleks dalam kehidupan nyata.
Dalam konteks operasi matriks, pemahaman yang komprehensif dapat diperoleh melalui pengerjaan contoh soal. Begitu pula dalam bidang bahasa, contoh soal memainkan peran penting, seperti pada contoh soal kalimat acak yang menguji kemampuan menyusun dan mengidentifikasi kalimat yang benar. Dengan mengerjakan contoh soal operasi matriks maupun contoh soal kalimat acak, siswa dapat mengasah keterampilan analitis dan menguji pemahaman mereka secara mendalam.
Contoh Soal Operasi Matriks
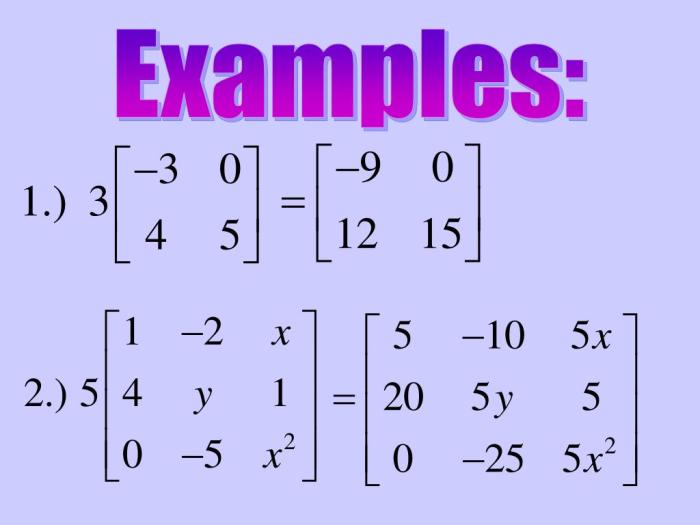
Untuk memahami operasi matriks dengan lebih baik, mari kita selesaikan beberapa contoh soal.
Contoh Soal Tingkat Dasar
- Diketahui matriks A = [[2, 1], [3, 4]] dan B = [[5, 6], [7, 8]]. Hitunglah A + B.
- Diketahui matriks C = [[1, 2, 3], [4, 5, 6]]. Tentukan determinan matriks C.
Contoh Soal Tingkat Menengah
- Diketahui matriks D = [[1, 2], [3, 4]] dan E = [[5, 6], [7, 8]]. Hitunglah D – E.
- Diketahui matriks F = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]. Tentukan invers matriks F.
Contoh Soal Tingkat Lanjutan
- Diketahui matriks G = [[1, 2], [3, 4]] dan H = [[5, 6], [7, 8]]. Tentukan nilai eigen dan vektor eigen matriks G – H.
- Diketahui matriks I = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]. Tentukan pangkat matriks I.
Kesulitan Umum
Beberapa kesulitan umum yang dihadapi siswa dalam menyelesaikan contoh soal operasi matriks meliputi:
- Kesalahan dalam perhitungan aljabar dasar
- Kesulitan dalam memahami konsep determinan dan invers
- Ketidakmampuan untuk mengidentifikasi nilai eigen dan vektor eigen
- Kesulitan dalam menghitung pangkat matriks
Dengan berlatih secara teratur dan memahami konsep-konsep yang mendasari, siswa dapat mengatasi kesulitan ini dan menjadi mahir dalam menyelesaikan operasi matriks.
5. Tips Menyelesaikan Operasi Matriks

Operasi matriks melibatkan perhitungan yang dapat memakan waktu dan kompleks. Berikut adalah beberapa tips untuk menyelesaikan operasi matriks secara efisien:
Menggunakan Sifat Matriks
Memahami sifat-sifat matriks, seperti sifat komutatif, asosiatif, dan distributif, dapat menyederhanakan perhitungan. Misalnya, sifat komutatif untuk penjumlahan matriks memungkinkan Anda menukar urutan penjumlahan tanpa memengaruhi hasilnya.
Menyederhanakan Matriks
Menyederhanakan matriks dengan melakukan operasi seperti mengubah baris atau kolom menjadi nol dapat mengurangi jumlah perhitungan yang diperlukan. Misalnya, mengubah baris matriks menjadi baris nol memungkinkan Anda mengurangi perhitungan perkalian dengan nol.
Menggunakan Matriks Identitas
Matriks identitas, yaitu matriks persegi dengan 1 pada diagonal utama dan 0 pada elemen lainnya, dapat menyederhanakan perhitungan tertentu. Misalnya, mengalikan matriks dengan matriks identitas tidak mengubah matriks asli.
Membagi Perhitungan
Untuk operasi matriks yang kompleks, memecah perhitungan menjadi langkah-langkah yang lebih kecil dapat membuat prosesnya lebih mudah dikelola. Misalnya, memecah perkalian matriks menjadi perkalian baris dan kolom dapat mengurangi jumlah perhitungan.
Menggunakan Kalkulator Matriks
Kalkulator matriks online atau perangkat lunak dapat mengotomatiskan perhitungan matriks, menghemat waktu dan mengurangi kemungkinan kesalahan. Namun, pastikan untuk memverifikasi hasil secara manual untuk memastikan akurasi.
Pemungkas

Dengan pemahaman yang baik tentang contoh soal operasi matriks, individu dapat mengembangkan keterampilan analitis yang kuat dan kemampuan pemecahan masalah yang efektif. Operasi matriks terus menjadi alat yang sangat diperlukan dalam bidang teknik, ekonomi, dan sains, membuka jalan bagi kemajuan dan inovasi yang berkelanjutan.
Pertanyaan yang Kerap Ditanyakan
Apa itu contoh soal operasi matriks?
Contoh soal operasi matriks adalah masalah yang diberikan untuk melatih keterampilan dalam melakukan operasi penjumlahan, pengurangan, perkalian, dan perkalian skalar pada matriks.
Bagaimana cara menyelesaikan contoh soal operasi matriks?
Untuk menyelesaikan contoh soal operasi matriks, ikuti langkah-langkah berikut: identifikasi jenis operasi yang diperlukan, lakukan operasi pada setiap elemen matriks, dan verifikasi hasilnya.
Apa kesulitan umum dalam menyelesaikan contoh soal operasi matriks?
Kesulitan umum meliputi kesalahan perhitungan, kesalahan dalam mengidentifikasi jenis operasi, dan kesulitan dalam menangani matriks berukuran besar.
