Contoh soal aljabar matriks adalah kunci untuk menguasai konsep penting dalam aljabar linier. Dalam panduan komprehensif ini, kita akan menjelajahi berbagai jenis matriks, operasi dasar, dan teknik penyelesaian untuk beragam masalah dunia nyata.
Dari menentukan determinan hingga mencari matriks invers, panduan ini akan membekali Anda dengan pemahaman mendalam tentang aljabar matriks, sehingga membuka jalan untuk aplikasi yang lebih luas dalam berbagai bidang.
Konsep Dasar Aljabar Matriks

Matriks merupakan susunan bilangan-bilangan yang disusun dalam baris dan kolom. Notasi untuk menyatakan matriks adalah A = [a ij], dimana a ijadalah elemen pada baris ke-i dan kolom ke-j.
Ukuran dan Bentuk Matriks
Ukuran matriks ditentukan oleh jumlah baris dan kolomnya. Matriks dengan m baris dan n kolom disebut matriks m x n. Bentuk matriks mengacu pada susunan baris dan kolomnya, seperti matriks persegi (jumlah baris sama dengan jumlah kolom), matriks persegi panjang (jumlah baris tidak sama dengan jumlah kolom), atau matriks diagonal (elemen-elemen di luar diagonal utama bernilai 0).
Operasi Dasar Matriks
- Penjumlahan:Dua matriks dengan ukuran yang sama dapat dijumlahkan dengan menjumlahkan elemen-elemen yang berada pada posisi yang sama.
- Pengurangan:Dua matriks dengan ukuran yang sama dapat dikurangkan dengan mengurangkan elemen-elemen yang berada pada posisi yang sama.
- Perkalian:Perkalian matriks melibatkan perkalian elemen-elemen baris pada matriks pertama dengan elemen-elemen kolom pada matriks kedua, dan menjumlahkan hasilnya. Hasil perkalian matriks hanya dapat dilakukan jika jumlah kolom pada matriks pertama sama dengan jumlah baris pada matriks kedua.
Determinan Matriks
Determinan adalah sebuah nilai numerik yang terkait dengan matriks persegi. Ini memberikan informasi penting tentang matriks, seperti apakah matriks tersebut memiliki invers atau tidak.
Definisi dan Rumus
Determinan dari matriks persegi A = [a ij] n x ndidefinisikan sebagai:
det(A) = ∑i=1na i1C i1
di mana C i1adalah kofaktor dari a i1.
Sifat-sifat Determinan
- det(A -1) = 1/det(A)
- det(kA) = k ndet(A), untuk k bilangan real
- det(A T) = det(A)
- det(AB) = det(A)det(B)
Contoh Perhitungan Determinan Matriks
Misalkan kita memiliki matriks:
| 1 | 2 |
| 3 | 4 |
Determinan matriks ini adalah:
det(A) = 1
- 4
- 2
- 3 =
- 2
Matriks Invers

Matriks invers adalah matriks yang dapat digunakan untuk membatalkan operasi perkalian matriks. Matriks invers hanya dapat dihitung untuk matriks persegi (matriks yang jumlah baris dan kolomnya sama).
Dalam mempelajari aljabar matriks, terdapat berbagai contoh soal yang dapat membantu mengasah pemahaman. Salah satu contoh soal yang umum adalah mencari invers matriks. Untuk memperluas pengetahuan tentang contoh soal, kita dapat merujuk pada contoh soal pph dan jawabannya. Dari soal tersebut, kita dapat mempelajari cara menghitung pajak penghasilan dan memahami berbagai ketentuan yang berlaku.
Kembali ke topik aljabar matriks, contoh soal lain yang menarik adalah menentukan determinan matriks, yang dapat digunakan untuk mengetahui apakah suatu matriks inversnya ada atau tidak.
Matriks A dikatakan memiliki invers jika dan hanya jika determinannya tidak sama dengan nol.
Syarat-syarat Matriks Invers
- Matriks harus persegi.
- Determinan matriks tidak boleh nol.
Rumus Menghitung Matriks Invers
Rumus untuk menghitung invers dari matriks A berordo n adalah:
A -1= (1/det(A)) – C T
di mana:
- A -1adalah invers dari matriks A
- det(A) adalah determinan matriks A
- C Tadalah transpos dari kofaktor matriks A
Contoh Perhitungan Matriks Invers
Misalkan kita memiliki matriks A:
A =
Dalam ranah aljabar matriks, contoh soal kerap melibatkan operasi seperti penjumlahan, pengurangan, dan perkalian matriks. Pemahaman konsep ini sangat krusial untuk menyelesaikan soal yang lebih kompleks, seperti contoh soal mdof. Dalam konteks mdof, matriks digunakan untuk merepresentasikan sistem dengan banyak derajat kebebasan, sehingga menguasai operasi matriks menjadi prasyarat untuk menyelesaikan soal-soal mdof secara efektif.
Setelah menguasai konsep mdof, kembali ke contoh soal aljabar matriks akan memberikan perspektif baru dan memperdalam pemahaman tentang operasi matriks.
| 2 1 | </p> <p> | 3 2 | </p> <p>Determinan matriks A adalah:</p> <p>det(A) = (2- 2) – (1 – 3) = 1</p> <p>Kofaktor matriks A adalah:</p> Dalam aljabar matriks, kita dapat menemukan contoh soal yang mengasah keterampilan kita dalam memanipulasi matriks. Misalnya, kita dapat menghitung determinan matriks atau menyelesaikan sistem persamaan linear menggunakan matriks. Demikian pula, dalam ekonomi, kita juga dapat menemukan contoh soal yang menarik, seperti contoh soal biaya marginal. Soal-soal ini membantu kita memahami konsep biaya marginal dan cara menghitungnya dalam berbagai situasi bisnis. Dengan mempelajari kedua jenis soal ini, kita dapat memperdalam pemahaman kita tentang aljabar matriks dan prinsip-prinsip ekonomi. <p>C = | 2-1 | </p><p> | -3 2 | </p> <p>Transpos dari kofaktor matriks A adalah:</p> <p>C<sup>T</sup> = | 2-3 | </p><p> | -1 2 | </p> <p>Invers dari matriks A adalah:</p> <p>A<sup>-1</sup> = (1/1)- | 2-3 | </p><p> | -1 2 | </p> <p>A<sup>-1</sup> = | 2-3 | </p><p> | -1 2 |
|---|
Sistem Persamaan Linear
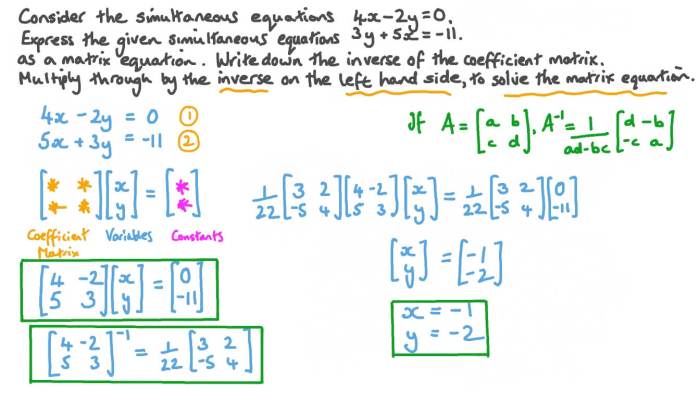
Sistem persamaan linear adalah kumpulan persamaan yang terdiri dari beberapa variabel. Sistem ini dapat diselesaikan menggunakan metode matriks, yang memungkinkan kita mewakilinya dalam bentuk matriks dan menggunakan operasi matriks untuk menemukan solusi.
Transformasi Sistem Persamaan Linear Menjadi Bentuk Matriks
Untuk mengubah sistem persamaan linear menjadi bentuk matriks, kita dapat menuliskannya sebagai berikut:
Ax = b
- A adalah matriks koefisien berukuran m x n, di mana m adalah jumlah persamaan dan n adalah jumlah variabel.
- x adalah matriks kolom variabel berukuran n x 1.
- b adalah matriks kolom konstanta berukuran m x 1.
Metode Penyelesaian Sistem Persamaan Linear Menggunakan Matriks (Eliminasi Gauss-Jordan)
Eliminasi Gauss-Jordan adalah metode untuk menyelesaikan sistem persamaan linear menggunakan operasi matriks. Operasi ini meliputi:
- Pertukaran baris
- Perkalian baris dengan skalar
- Penambahan baris
Dengan menggunakan operasi ini, kita dapat mengubah matriks A menjadi matriks identitas dan matriks b menjadi matriks kolom solusi.
Contoh Penyelesaian Sistem Persamaan Linear
Misalkan kita memiliki sistem persamaan linear berikut:
2x + 3y = 12
x – y = 1
Kita dapat menulis sistem ini dalam bentuk matriks sebagai berikut:
[2 3] [x] = [12]
[1 -1] [y] = [1]
Dengan menggunakan eliminasi Gauss-Jordan, kita dapat menyelesaikan sistem ini sebagai berikut:
[1 0] [x] = [4]
[0 1] [y] = [1]
Jadi, solusi dari sistem persamaan linear tersebut adalah x = 4 dan y = 1.
Transformasi Geometri
Dalam geometri koordinat, matriks transformasi memainkan peran penting dalam merepresentasikan dan menerapkan transformasi geometri. Transformasi geometri adalah operasi yang memetakan titik atau bentuk pada bidang atau ruang ke lokasi atau orientasi baru.
Matriks transformasi geometri dapat digunakan untuk merepresentasikan berbagai jenis transformasi, seperti translasi, rotasi, dan skala.
Matriks Transformasi Translasi
Matriks transformasi translasi menggeser titik pada bidang atau ruang dengan jarak tertentu dalam arah tertentu. Bentuk umum dari matriks transformasi translasi adalah:
“`T = [1 0 tx] [0 1 ty] [0 0 1]“`
di mana `tx` dan `ty` adalah nilai translasi dalam arah x dan y, masing-masing.
Matriks Transformasi Rotasi
Matriks transformasi rotasi memutar titik pada bidang atau ruang dengan sudut tertentu di sekitar titik asal. Bentuk umum dari matriks transformasi rotasi adalah:
“`R = [cos(theta)
sin(theta) 0]
[sin(theta) cos(theta) 0] [0 0 1]“`
di mana `theta` adalah sudut rotasi dalam radian.
Matriks Transformasi Skala
Matriks transformasi skala memperbesar atau memperkecil titik pada bidang atau ruang dengan faktor tertentu. Bentuk umum dari matriks transformasi skala adalah:
“`S = [sx 0 0] [0 sy 0] [0 0 1]“`
di mana `sx` dan `sy` adalah faktor skala dalam arah x dan y, masing-masing.
Penerapan Matriks Transformasi dalam Geometri Koordinat, Contoh soal aljabar matriks
Matriks transformasi digunakan secara luas dalam geometri koordinat untuk menyelesaikan berbagai masalah, seperti:
- Mencari koordinat titik setelah ditransformasikan
- Menemukan persamaan garis atau kurva setelah ditransformasikan
- Menganalisis sifat transformasi geometri
Contoh Penggunaan Matriks Transformasi
Berikut adalah contoh penggunaan matriks transformasi dalam geometri koordinat:
- Translasi:Menerjemahkan titik (2, 3) dengan jarak 4 unit ke kanan dan 2 unit ke bawah dapat direpresentasikan dengan matriks transformasi:
“` T = [1 0 4] [0 1 2] [0 0 1] “`
- Rotasi:Memutar titik (3, -2) dengan sudut 45 derajat berlawanan arah jarum jam di sekitar titik asal dapat direpresentasikan dengan matriks transformasi:
“` R = [cos(45) -sin(45) 0] [sin(45) cos(45) 0] [0 0 1] “`
- Skala:Memperbesar titik (1, 2) dengan faktor 2 dalam arah x dan 3 dalam arah y dapat direpresentasikan dengan matriks transformasi:
“` S = [2 0 0] [0 3 0] [0 0 1] “`
Ruang Vektor

Dalam matematika, ruang vektor adalah struktur aljabar yang terdiri dari sekumpulan vektor yang dapat dijumlahkan dan dikalikan dengan skalar. Ruang vektor digunakan secara luas dalam berbagai bidang, termasuk fisika, teknik, dan ilmu komputer.
Basis Vektor
Basis vektor adalah sekumpulan vektor yang digunakan untuk merepresentasikan setiap vektor dalam ruang vektor. Vektor dalam ruang vektor dapat ditulis sebagai kombinasi linear dari vektor-vektor basis.
Operasi pada Vektor
- Penjumlahan Vektor:Dua vektor dapat dijumlahkan dengan menambahkan komponen-komponennya.
- Perkalian Skalar:Vektor dapat dikalikan dengan skalar (bilangan real) untuk menghasilkan vektor baru yang sejajar dengan vektor asli tetapi dengan panjang yang berbeda.
Representasi Vektor Menggunakan Matriks
Vektor dapat direpresentasikan menggunakan matriks kolom. Misalnya, vektor dengan komponen (a, b, c) dapat direpresentasikan sebagai matriks berikut:
[a][b] [c]
Ruang Vektor Ortogonal

Ruang vektor ortogonal adalah ruang vektor yang terdiri dari vektor-vektor yang saling ortogonal, atau tegak lurus satu sama lain. Ruang vektor ortogonal memainkan peran penting dalam berbagai aplikasi, seperti geometri, fisika, dan teknik.
Sifat-Sifat Ruang Vektor Ortogonal
- Vektor nol adalah ortogonal terhadap semua vektor di ruang.
- Dua vektor yang ortogonal memiliki hasil kali titik nol.
- Jika suatu vektor ortogonal terhadap dua vektor yang saling ortogonal, maka vektor tersebut juga ortogonal terhadap semua kombinasi linear dari kedua vektor tersebut.
- Setiap ruang vektor berdimensi hingga memiliki basis ortonormal, yaitu basis yang terdiri dari vektor-vektor yang saling ortogonal dan memiliki norma 1.
Proyeksi Vektor dan Matriks Proyeksi
Proyeksi vektor uke arah vektor vadalah vektor projvu yang sejajar dengan vdan memiliki panjang sama dengan
| <strong>u</strong> |
|---|
cos(θ), di mana θ adalah sudut antara udan v.
Matriks proyeksi Pvadalah matriks yang memproyeksikan setiap vektor ke arah v. Matriks ini dapat dinyatakan sebagai:
Pv= (v Tv) -1v T
Penerapan Ruang Vektor Ortogonal dalam Aplikasi Dunia Nyata
- Geometri:Ruang vektor ortogonal digunakan untuk merepresentasikan dan menganalisis objek geometris, seperti garis, bidang, dan volume.
- Fisika:Ruang vektor ortogonal digunakan dalam mekanika kuantum untuk merepresentasikan keadaan sistem kuantum.
- Teknik:Ruang vektor ortogonal digunakan dalam pengolahan sinyal dan kompresi data.
Matriks Eigen
Matriks eigen adalah matriks persegi yang memiliki sifat unik yaitu ketika dikalikan dengan vektor eigennya, hasilnya akan menghasilkan vektor eigen yang sama namun dikalikan dengan nilai skalar yang disebut nilai eigen.
Dalam mempelajari aljabar matriks, contoh soal memainkan peran penting dalam mengasah keterampilan. Untuk memperluas sumber latihan, tersedia banyak contoh soal online yang dapat diakses secara mudah. Contoh soal online ini menawarkan variasi soal yang komprehensif, mulai dari soal dasar hingga soal yang lebih menantang, sehingga membantu siswa menguji pemahaman mereka secara mendalam tentang konsep aljabar matriks.
Sifat-sifat Matriks Eigen
- Nilai eigen suatu matriks adalah akar karakteristik matriks tersebut.
- Setiap nilai eigen memiliki satu atau lebih vektor eigen yang sesuai.
- Vektor eigen dari matriks yang berbeda-beda dapat saling ortogonal.
- Matriks eigen dapat didekomposisi menjadi perkalian matriks diagonal (berisi nilai eigen) dengan matriks yang berisi vektor eigen.
Metode Mencari Nilai Eigen dan Vektor Eigen
Untuk mencari nilai eigen dan vektor eigen suatu matriks, dapat digunakan beberapa metode, antara lain:
- Metode Persamaan Karakteristik
- Metode Daya
- Metode QR
Penerapan Matriks Eigen
Matriks eigen memiliki banyak penerapan dalam berbagai bidang, antara lain:
- Analisis stabilitas sistem
- Pengenalan pola
- Kompresi gambar
- Kriptografi
Aplikasi Aljabar Matriks
Aljabar matriks memiliki aplikasi luas dalam berbagai bidang, termasuk ilmu komputer, fisika, dan ekonomi.
Aplikasi dalam Ilmu Komputer
- Grafik Komputer:Matriks transformasi digunakan untuk menerjemahkan, memutar, dan menskalakan objek dalam ruang 3D.
- Pemrosesan Sinyal:Matriks digunakan dalam pemrosesan gambar, pengenalan pola, dan analisis suara.
Aplikasi dalam Fisika
- Mekanika Kuantum:Matriks digunakan untuk mewakili operator dan keadaan dalam mekanika kuantum.
- Elektromagnetisme:Matriks digunakan untuk menyelesaikan persamaan Maxwell dan menganalisis medan elektromagnetik.
Aplikasi dalam Ekonomi
- Analisis Data:Matriks digunakan untuk menyimpan dan menganalisis data ekonomi, seperti harga saham dan tren inflasi.
- Peramalan:Matriks digunakan dalam model ekonometrik untuk meramalkan tren ekonomi dan membuat keputusan investasi.
Ringkasan Penutup: Contoh Soal Aljabar Matriks
Dengan menguasai contoh soal aljabar matriks, Anda tidak hanya akan memperkuat keterampilan matematika Anda, tetapi juga memperoleh alat yang ampuh untuk memecahkan masalah kompleks di berbagai bidang, mulai dari ilmu komputer hingga fisika dan ekonomi.
Daftar Pertanyaan Populer
Apa itu matriks?
Matriks adalah susunan angka yang diatur dalam baris dan kolom.
Bagaimana cara menghitung determinan matriks?
Determinan adalah ukuran besaran matriks, dan dapat dihitung menggunakan rumus khusus.
Apa itu matriks invers?
Matriks invers adalah matriks yang ketika dikalikan dengan matriks asli menghasilkan matriks identitas.
