Contoh soal himpunan matematika kuliah memberikan landasan yang kokoh untuk memahami konsep dasar teori himpunan, yang menjadi dasar berbagai bidang matematika.
Dalam panduan ini, kita akan mengeksplorasi konsep penting seperti operasi himpunan, relasi dan fungsi, kardinalitas, himpunan daya, dan aplikasi himpunan dalam berbagai bidang matematika.
Konsep Dasar Himpunan
Himpunan adalah kumpulan objek yang berbeda dan terdefinisi dengan jelas. Objek-objek ini disebut anggota himpunan, dan himpunan itu sendiri biasanya dilambangkan dengan huruf kapital, seperti A, B, atau C.
Jenis-Jenis Himpunan
- Himpunan Kosong:Himpunan yang tidak memiliki anggota, dilambangkan dengan Ø atau .
- Himpunan Hingga:Himpunan yang memiliki jumlah anggota yang terbatas.
- Himpunan Tak Hingga:Himpunan yang memiliki jumlah anggota yang tidak terbatas.
- Himpunan Bagian:Himpunan yang semua anggotanya juga merupakan anggota dari himpunan lain.
- Himpunan Universal:Himpunan yang berisi semua objek yang relevan dalam konteks tertentu.
Contoh Himpunan dalam Kehidupan Sehari-hari
- Himpunan siswa di kelas
- Himpunan buah-buahan yang ada di pasar
- Himpunan bilangan genap
Operasi-Operasi Himpunan
Gabungan Himpunan
Gabungan dari dua himpunan A dan B, dilambangkan dengan A ∪ B, adalah himpunan yang berisi semua anggota A dan semua anggota B.
Dalam menyelesaikan contoh soal himpunan matematika kuliah, pemahaman tentang penggunaan article a, an, dan the sangat penting. Seperti halnya pada contoh soal article a an the , kita harus memperhatikan konteks dan makna yang ingin disampaikan. Dalam contoh soal himpunan matematika, article yang tepat dapat membantu menentukan apakah anggota himpunan tertentu termasuk atau tidak dalam himpunan tersebut.
Irisan Himpunan
Irisan dari dua himpunan A dan B, dilambangkan dengan A ∩ B, adalah himpunan yang berisi semua anggota yang merupakan anggota A dan juga anggota B.
Komplemen Himpunan
Komplemen dari himpunan A dalam himpunan universal U, dilambangkan dengan A c, adalah himpunan yang berisi semua anggota U yang bukan anggota A.
Dalam ranah matematika kuliah, mahasiswa dihadapkan pada berbagai contoh soal himpunan yang menguji pemahaman mereka tentang konsep-konsep fundamental. Sebagai bagian dari persiapan yang komprehensif, mahasiswa juga perlu menguasai bahasa arab sebagai alat komunikasi dalam bidang keilmuan. Situs contoh soal bahasa arab untuk mahasiswa menyediakan beragam latihan soal yang efektif untuk mengasah keterampilan berbahasa arab.
Dengan menguasai contoh soal himpunan matematika kuliah dan contoh soal bahasa arab untuk mahasiswa, mahasiswa dapat memperkaya pengetahuan mereka di kedua bidang ini dan mempersiapkan diri dengan baik untuk tantangan akademis di masa depan.
Relasi dan Fungsi: Contoh Soal Himpunan Matematika Kuliah
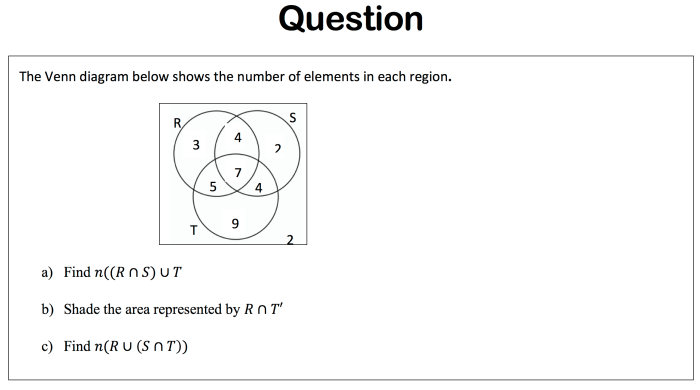
Dalam matematika, relasi dan fungsi adalah konsep dasar yang digunakan untuk memodelkan hubungan antara dua atau lebih himpunan.
Relasi, Contoh soal himpunan matematika kuliah
Relasi adalah hubungan antara dua himpunan, A dan B, yang dilambangkan sebagai R ⊆ A × B. Relasi ini dapat dilihat sebagai himpunan pasangan berurutan (a, b) di mana a ∈ A dan b ∈ B.
- Relasi Reflektif:Relasi yang memuat pasangan (a, a) untuk semua a ∈ A.
- Relasi Simetris:Relasi yang memuat pasangan (a, b) jika dan hanya jika pasangan (b, a) juga terdapat.
- Relasi Transitif:Relasi yang memuat pasangan (a, c) jika terdapat pasangan (a, b) dan (b, c) dalam relasi.
Fungsi
Fungsi adalah relasi khusus yang memuat setiap elemen dari himpunan A ke tepat satu elemen dari himpunan B. Fungsi ini dilambangkan sebagai f: A → B, dan setiap elemen a ∈ A memiliki pasangan unik b ∈ B yang ditulis sebagai f(a) = b.
- Fungsi Injektif:Fungsi yang memetakan elemen yang berbeda dari A ke elemen yang berbeda dari B.
- Fungsi Surjektif:Fungsi yang memetakan setiap elemen dari B ke setidaknya satu elemen dari A.
- Fungsi Bijektif:Fungsi yang bersifat injektif dan surjektif.
Kardinalitas Himpunan
Kardinalitas himpunan adalah ukuran dari jumlah elemen dalam suatu himpunan. Himpunan dapat memiliki kardinalitas berhingga atau tak berhingga.
Menghitung Kardinalitas Himpunan Berhingga
Kardinalitas himpunan berhingga dapat dihitung dengan cara menghitung jumlah elemennya secara langsung. Misalnya, himpunan 1, 2, 3 memiliki kardinalitas 3.
Menghitung Kardinalitas Himpunan Tak Berhingga
Kardinalitas himpunan tak berhingga tidak dapat dihitung dengan cara yang sama seperti himpunan berhingga. Namun, terdapat beberapa metode yang dapat digunakan untuk menentukan kardinalitas himpunan tak berhingga, salah satunya adalah menggunakan bilangan kardinal.
Dalam mempelajari himpunan matematika di tingkat perkuliahan, mahasiswa sering kali berlatih mengerjakan soal-soal untuk menguji pemahaman mereka. Salah satu jenis soal yang umum diberikan adalah soal tentang menentukan anggota himpunan dan operasi himpunan. Untuk mengasah keterampilan ini, mahasiswa dapat merujuk pada berbagai sumber soal latihan, termasuk contoh soal utbk soshum 2020 pdf dan pembahasannya.
Dengan berlatih mengerjakan soal-soal tersebut, mahasiswa dapat mempersiapkan diri untuk menghadapi soal-soal serupa dalam ujian himpunan matematika kuliah.
Teorema-Teorema Kardinalitas
- Hukum De Morgan: Jika A dan B adalah himpunan, maka kardinalitas irisan (A ∩ B) ditambah kardinalitas gabungan (A ∪ B) sama dengan jumlah kardinalitas A dan B.
- Teorema Cantor-Bernstein-Shroeder: Jika terdapat fungsi injektif dari A ke B dan fungsi surjektif dari B ke A, maka A dan B memiliki kardinalitas yang sama.
Himpunan Daya dan Ruang Topologi
Himpunan daya dan ruang topologi adalah konsep penting dalam matematika. Himpunan daya mengacu pada himpunan semua himpunan bagian dari suatu himpunan tertentu, sedangkan ruang topologi adalah himpunan yang dilengkapi dengan struktur tambahan yang disebut topologi.
Contoh soal himpunan matematika kuliah kerap menguji pemahaman mahasiswa tentang konsep dasar himpunan. Namun, untuk memperluas pengetahuan vektor, mahasiswa dapat mempelajari 20 contoh soal un vektor matematika dan pembahasannya yang tersedia pada tautan ini. Soal-soal tersebut akan membantu mahasiswa memahami sifat-sifat vektor, operasi vektor, dan aplikasi vektor dalam berbagai bidang.
Dengan demikian, mahasiswa dapat memperdalam pemahaman mereka tentang himpunan dan vektor, yang merupakan topik penting dalam matematika kuliah.
Sifat-sifat Himpunan Daya
- Himpunan daya dari himpunan kosong adalah himpunan kosong.
- Himpunan daya dari himpunan berhingga dengan nelemen memiliki 2 nelemen.
- Himpunan daya dari himpunan tak hingga adalah himpunan tak hingga.
Sifat-sifat Ruang Topologi
- Ruang topologi memiliki himpunan terbuka yang memenuhi sifat-sifat tertentu, seperti himpunan kosong dan himpunan itu sendiri adalah terbuka, gabungan dari himpunan terbuka adalah terbuka, dan perpotongan dari sejumlah hingga himpunan terbuka adalah terbuka.
- Topologi pada suatu himpunan unik untuk himpunan tersebut.
- Ruang topologi dapat diklasifikasikan menjadi beberapa jenis, seperti ruang metrik, ruang Hausdorff, dan ruang kompak.
Contoh Himpunan Daya
- Himpunan daya dari himpunan 1, 2 adalah , 1, 2, 1, 2.
- Himpunan daya dari himpunan bilangan asli adalah himpunan semua himpunan bilangan asli.
Contoh Ruang Topologi
- Himpunan bilangan real dengan topologi standar, di mana himpunan terbuka adalah interval dan gabungannya.
- Himpunan titik pada garis dengan topologi diskrit, di mana setiap titik adalah himpunan terbuka.
Aplikasi Himpunan dalam Matematika
Himpunan memainkan peran penting dalam berbagai bidang matematika, menyediakan landasan untuk konsep dan operasi matematika yang kompleks. Berikut ini adalah beberapa aplikasi himpunan dalam matematika:
Teori Bilangan
Dalam teori bilangan, himpunan digunakan untuk mendefinisikan konsep-konsep seperti bilangan prima, bilangan genap, dan bilangan ganjil. Misalnya, himpunan bilangan prima adalah himpunan semua bilangan asli yang lebih besar dari 1 dan hanya habis dibagi 1 dan dirinya sendiri.
Aljabar
Dalam aljabar, himpunan digunakan untuk mendefinisikan struktur seperti grup, gelanggang, dan medan. Misalnya, grup adalah himpunan dengan operasi yang menggabungkan dua elemen dari himpunan tersebut untuk menghasilkan elemen ketiga dalam himpunan yang sama.
Analisis
Dalam analisis, himpunan digunakan untuk mendefinisikan konsep seperti limit, turunan, dan integral. Misalnya, limit fungsi adalah nilai yang didekati oleh fungsi saat input mendekati nilai tertentu. Limit ini dapat didefinisikan sebagai himpunan semua nilai output yang dapat dicapai oleh fungsi saat input mendekati nilai tertentu.
Contoh Soal
Berikut ini adalah beberapa contoh soal matematika yang melibatkan konsep himpunan:
- Tentukan himpunan semua bilangan genap yang lebih besar dari 10 dan kurang dari 20.
- Misalkan A = 1, 2, 3, 4 dan B = 3, 4, 5, 6. Tentukan irisan dan gabungan dari himpunan A dan B.
- Tentukan apakah himpunan berikut merupakan grup: G = 1, -1, i, -i dengan operasi perkalian kompleks.
Tabel Aplikasi Himpunan dalam Matematika
| Bidang Matematika | Aplikasi Himpunan |
|---|---|
| Teori Bilangan | Definisi bilangan prima, bilangan genap, bilangan ganjil |
| Aljabar | Definisi grup, gelanggang, medan |
| Analisis | Definisi limit, turunan, integral |
Ringkasan Terakhir
Menguasai contoh soal himpunan matematika kuliah tidak hanya memperkuat pemahaman teoretis tetapi juga melatih keterampilan pemecahan masalah yang penting untuk kesuksesan di bidang matematika.
Informasi FAQ
Apa manfaat mempelajari contoh soal himpunan matematika kuliah?
Membantu memahami konsep dasar teori himpunan, meningkatkan keterampilan pemecahan masalah, dan mempersiapkan mahasiswa untuk aplikasi himpunan dalam berbagai bidang matematika.
Apakah ada persyaratan khusus untuk mempelajari contoh soal himpunan matematika kuliah?
Pemahaman dasar tentang matematika sekolah menengah, khususnya aljabar dan logika, akan bermanfaat.
